前言

上一篇我們介紹了『購物籃分析』的觀念與實作，現在就來研究它背後的演算法 -- Apriori，是如何找到這些關聯性強的商品組合。

Apriori 原理

『Apriori Algorithm — Know How to Find Frequent Itemsets』 一文有很棒的介紹，以下的圖都是來自這篇文章。

1. 購買記錄如下，第1欄是交易代碼(TID)，第2欄是購買的商品(Items)：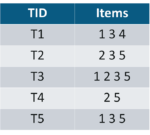
   

2. Apriori演算法需要設定最小支持度(min_support)，以過濾掉不暢銷的商品，假設為2，第四項商品會被濾掉：
   
   結果如下：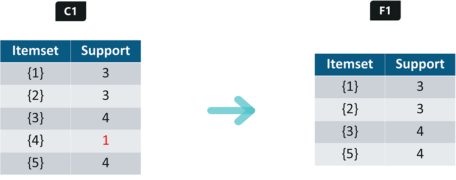
   

3. 找出含2項商品的所有組合，如下，再算一次Support，一樣過濾掉『Support<2』的商品組合，結果稱為F2：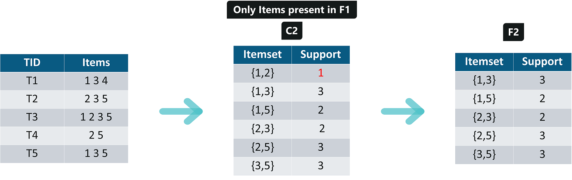
   

4. 找出含3項商品的所有組合，注意，先排除沒有在F2表中的組合，只要組合中的任兩項商品不在F2中，那該項3合一商品的組合就會被過濾掉。
   
   結果如下：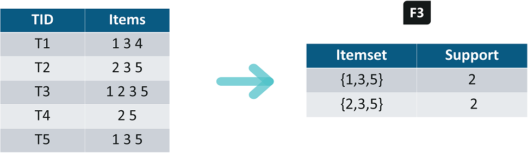
   

5. 由於只剩兩項3合一商品組合，我們就直接把它們合併，只有一項4合一商品組合，計算Support，小於2，直接過濾掉。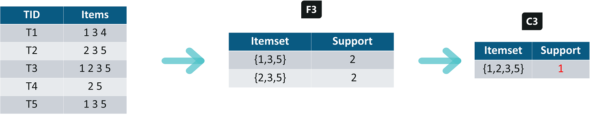
   

第4、5步驟，為什麼要部分集合不符的組合過濾掉，這是基於Apriori兩個定理：

1. 假設一個集合{A,B}大於最小支持度(Min_Support)，則它的子集合{A},{B}出現次數必定大於最小支持度。
2. 假設集合{A}出現次數小於最小支持度，則它與其他商品的集合，如{A,B}，必定小於最小支持度。

接著，把合於條件的商品組合，分別計算各項統計量，再進一步篩選即可。

Association Rules

假設顧客買了商品組合中的部份商品，是否應推薦組合中的其他商品給顧客，這就是所謂的『Association Rules』，我們可以訂定最小信心度(min_confidence)，譬如 60%，我們以 {1,3,5} 商品組合為例：

1. 顧客買{1,3}，是否推薦 5?
   Confidence = support(1,3,5)/support(1,3) = 2/3 = 66.66% > 60% (推薦)

2. 顧客買{1,5}，是否推薦 3?
   Confidence = support(1,3,5)/support(1,5) = 2/2 = 100% > 60% (強烈推薦)

3. 顧客買{3,5}，是否推薦 1?
   Confidence = support(1,3,5)/support(3,5) = 2/3 = 66.66% > 60% (推薦)

4. 顧客買{1}，是否推薦 {3,5}?
   Confidence = support(1,3,5)/support(1) = 2/3 = 66.66% > 60% (推薦)

5. 顧客買{3}，是否推薦 {1,5}?
   Confidence = support(1,3,5)/support(3) = 2/4 = 50% < 60% (不推薦)

6. 顧客買{5}，是否推薦 {1,3}?
   Confidence = support(1,3,5)/support(5) = 2/4 = 50% < 60% (不推薦)

依此類推，我們就可以找出所有的推薦規則了。

另外一篇『Frequent Itemsets via Apriori Algorithm』也是值得推薦的好文，它說明每個實作的步驟。

結論

購物籃分析是一個很簡單、實用的推薦方法，不過，需要反覆掃描資料庫，考慮各種組合，若品項很多的時候，執行計算的時間會很久。接下來，我們就來繼續看看其他推薦系統的演算法。

筆者註冊了Coursera『Recommendation Systems with TensorFlow on GCP』線上課程，之後就現學現賣，將心得記錄下來，與大家分享。